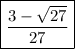Question

Help me out please. I need ASAP

Answer 1

`\displaystyle (3-√(27))/(27)`

Explanation:

Simplifying Roots

When roots are found in an algebraic expression, it's convenient to recall these properties:

`\displaystyle \sqrt[m]{x^n}=\ x^{(n)/(m)}`

`\displaystyle x^m.\ x^n=\ x^(m+n)`

`\displaystyle (x^m)^n=\ x^(m.n)`

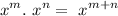
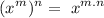
The expression is given as

`\displaystyle \frac{\sqrt[4]{9}-√(9)}{\sqrt[4]{9^5}}`

We know that
`9=3^2`, so

`\displaystyle \frac{\sqrt[4]{3^2}-√(3^2)}{\sqrt[4]{3^(10)}}`

Applying the root property

`\displaystyle \frac{3^(2)/(4)-3^{(2)/(2)}}{3^(10)/(4)}`

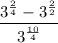
Simplifying the fractions

`\displaystyle (3^(1)/(2)-3^1)/(3^(5)/(2))`

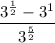
Multiplying both parts by
`3^(1/2)`

`\displaystyle (3^(1)/(2)(3^(1)/(2)-3^1))/(3^(1)/(2)\ 3^(5)/(2))`

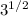
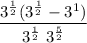
Operating the exponents

`\displaystyle \frac{3^{(1)/(2)+(1)/(2)}-3^{1+(1)/(2)}}{3^{(1)/(2)+(5)/(2)}}`

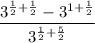
Or equivalently

`\displaystyle (3^1-3^(3)/(2))/(3^(6)/(2))`

Simplifying and converting back to root notation

`\displaystyle (3-√(3^3))/(3^3)`

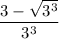
Operating

`\boxed{\displaystyle (3-√(27))/(27)}`