Question

Your friend provides a solution to the following problem. Evaluate her solution. The problem: Jim (mass 50 kg) steps off a ledge that is 2.0 m above a platform that sits on top of a relaxed spring of force constant 8000 N/m. How far will the spring compress while stopping Jim? Your friend's solution: (50kg)(9.8m/s2)(2.0m)=(1/2)(8000N/m)x x=0.25m

Answer 1

`\Delta x=61.25\ mm`

Step-by-step explanation:

Given:

• height of the ledge placed on a spring,
  `h=2\ m`

• stiffness of the spring,
  `k=8000\ N.m^(-1)`

• mass of the body placed over the ledge,
  `m=50\ kg`

Now the load on the spring due to body weight:

`w=m.g`

`w=50* 9.8`

`w=490\ N`

As we know:

`F=k.\Delta x`

where F is the force of compression

`\Delta x=(w)/(k)`

`\Delta x=(490)/(8000)`

`\Delta x=0.06125\ m`

`\Delta x=61.25\ mm`

Answer 2

The compress of the spring is 0.495.

Step-by-step explanation:

Given that,

Mass = 50 kg

Spring constant = 8000 N/m

height = 2.0 m

We need to calculate the compress of the spring

Using law of conservation of energy

`mgh=(1)/(2)kx^2`

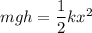
Where, m = mass

g = acceleration due to gravity

h = height

k = spring constant

x = distance

Put the value into the formula

`50*9.8*2.0=(1)/(2)*8000* x^2`

`x=\sqrt{(2*50*9.8*2.0)/(8000)}`

`x=0.495\ m`

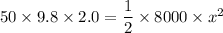
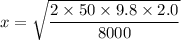
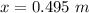
Hence, The compress of the spring is 0.495.