Question

The filament of a certain lamp has a resistance that increases linearly with temperature. When a constant voltage is switched on, the initial current decreases until the filament reaches its steady-state temperature. The temperature coefficient of resistivity of the filament is 4.5 times 10-3 K-1. The final current through the filament is one- eighth the initial current. What is the change in temperature of the filament?

a. 0100 K
b. 378 K
c. 1627 K
d. 814 K
e. 1162 K

Answer 1

To solve this problem we can apply the concept related to thermal expansion, including the analogy with resistance and final intensity.

The mathematical expression that describes the expansion of a material by a thermal process is given by

`R = R_0\alpha \Delta T`

Where

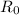`R_0`= Initial resistance

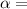`\alpha =` Thermal expansion coefficient

`\Delta T =` Change in the temperature

If we want to directly obtain the final value of the resistance of the object, you would simply add the initial resistance to this equation - because at this moment we have the result of how much resistance changed, but not of its final resistance - So,

`R_f = R_0 + L_0\alpha \Delta T`

`R_f = R_0(1 + \alpha \Delta T)`

Re-arrange to find the change at the temperature,

`\Delta T=(1)/(\alpha)(R_f)/(R_0)-1}`

Since the resistance is inversely proportional to the current and considering that the voltage is constant then

`R \propto (1)/(I)`

Then,

`\Delta T=(1)/(\alpha)(I_0)/(I_f)-1}`

`\Delta T = (1)/(4.5*10^(-3))((I_0)/(I_0/8)-1)`

`\Delta T = (1)/(4.5*10^(-3))(8-1)`

`\Delta T = 1555.5k`

(It is possible that there is a typing error and the value is not 4.5 but 4.3, so the closest approximate result would be 1627K and mark this as the correct answer)