Question

A puck company wants to sponsor the players with the 10% quickest goals in hockey games. The times of first goals are normally distributed with a mean of 12.56 minutes and a standard deviation of 4.91 minutes. How fast would a player need to make a goal to be sponsored by the puck company?

a. 6.27 minutes
b. 18.85 minutes
c. 17.47 minutes
d. 7.65 minutes

Answer 1

a. 6.27 minutes

Explanation:

Assuming a normal distribution. In order to be sponsored, a player must have a z-score corresponding to the 10th percentile of the normal curve.

At the 10th percentile, the z-score is -1.28.

Mean = 12.56 minutes

Standard Deviation = 4.91 minutes

The minimum value of X required is:

`z=(X-\mu)/(\sigma)\\ -1.28=(X-12.56)/(4.91)\\X= 6.27\ minutes`

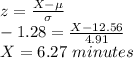
The player would need to make a goal within 6.27 minutes to be sponsored by the puck company