Question

The IQs of 700 applicants to a certain college are approximately normally distributed with a mean of 115 and a standard deviation of 11. If the college requires an IQ of at least 97, how many of these students will be rejected on this basis of IQ, regardless of their other qualificiations

Answer 1

Answer: 35

Explanation:

Given : The IQs of 700 applicants to a certain college are approximately normally distributed with a mean of 115 and a standard deviation of 11.

i.e.
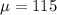`\mu=115` and
`\sigma= 11`

Let x denotes the IQs of applicants to college.

If the college requires an IQ of at least 97, then, the probability that students have IQ less than 97:-

`P(x<97)=P((x-\mu)/(\sigma)<(97-115)/(11))\\\\=P(z<-1.64) = 1-P(z<1.64)\ \ [\because\ P(Z<-z)=1-P(Z<z)]\\\\=1-0.9495=0.0505` [By using z-table]

Number of students will be rejected on this basis of IQ = Total students x Probability of students have IQ less than 97

= 700 x 0.0505 = 35.35 ≈ 35

Hence, about 35 students will be rejected on this basis of IQ, regardless of their other qualifications .