Question

A small motorboat travels 12 mph in still water. It takes 7 hours longer to travel 48 miles going upstream than it does going downstream. Find the rate of current. (Hint: 12+x= rate downstream and 12-x= rate upstream.)

Answer 1

Current rate of boat is 6.96 mph.

Explanation:

Given:

Distance traveled = 48 miles.

Time to travel = 7 hours

Speed of the boat in still water = 12 mph

We need to find the Current rate.

Let current rate be x;

Downstream rate =
`12+x`

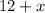
Upstream rate =
`12-x`

Now we know that Time is given by dividing Distance with Speed.

Hence Distance traveled is upstream and downstream.

Framing the equation we get;

`(48)/(12-x)-(48)/(12+x) = 7`

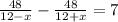
Now taking LCM we get;

`(48(12+x)-48(12-x))/((12+x)(12-x))=7\\\\576+48x-576+48x=7* (12+x)(12-x)\\96x=7*(144-x^2)\\96x=1008-7x^2\\7x^2+96x-1008=0`

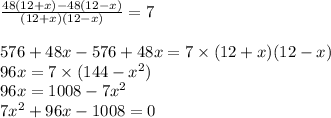
Now we will find the roots using quadratic formula.

a = 7 b =96 c =-1008

`b^2-4ac=96^2-4*7*-1008\\b^2-4ac=9216+28224 = 37440\\√(b^2-4ac) = √(37440) =193.49`

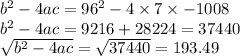
Now Quadratic formula is given by;

`x=(-b\±√(b^2-4ac))/(2a)`

`x_1= (-96+193.49)/(2*7) = 6.96\\\\x_2= (-96-193.49)/(2*7) = -20.67`

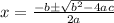
Now we have 2 values of x = 6.96 and x = -20.67

Since Speed of the boat cant be negative.

Hence we can say Current rate of boat is 6.96 mph