Answer:
neither
Explanation:
Parallel lines have equal slopes
The product of the slopes of perpendicular lines equals - 1
The equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
3x + 2y = 1 ( subtract 3x from both sides )
2y = - 3x + 1 ( divide each term by 2 )
y = -
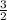 x +
x +
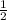 ← in slope- intercept form
← in slope- intercept form
with slope m = -
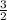
y = - x - 1 ← is in slope- intercept form
with slope m = - 1
Since the slopes are not equal then the lines are not parallel
-
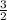 × - 1 =
× - 1 =
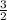 ≠ - 1
≠ - 1
Then the lines are not perpendicular