Question

The legs of a right triangle are measured as 40 centimeters and 80 centimeters, with the maximum error of 0.5 and 0.8 centimeters, respectively. The larger of the acute angles of the triangle is calculated as α=arctan(80/40). Use differentials to estimate the maximum error in the calculated value of α.

Answer 1

The maximum error in the calculated value of α is 0.00876712328767 radians.

Explanation:

Let us suppose the legs of the right triangle are x and y.

So, we have

x = 40 cm, y = 80 cm, dx = 0.5, dy = 0.8

We have to find maximum error in α for

`\alpha=(y)/(x)`

Now, find the differentials with respect to x and y

Partial differential of α with respect to x

`(\partial \alpha)/(\partial x)=(\partial )/(\partial x)(arctan\:\left((y)/(x)\right))\\\\(\partial \alpha)/(\partial y)=\-(y)/(y^2+x^2)}`

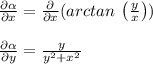
Similarly, partial differential of α with respect to y

`(\partial \alpha)/(\partial y)=(\partial )/(\partial y)(arctan\:\left((y)/(x)\right))\\\\(\partial \alpha)/(\partial y)=(x)/(y^2+x^2)`

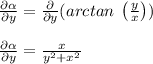
The maximum error in calculated value of α is given by

`d\alpha=\left | (\partial \alpha)/(\partial x)\cdot dx \right |+\left | (\partial \alpha)/(\partial y)\cdot dy \right |`

Substituting the known values, we get

`d\alpha=\left | -(80)/(80^2+30^2)\cdot 0.5 \right |+\left | (30)/(80^2+30^2)\cdot 0.8 \right |`

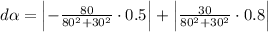
Simplifying, we get

`d\alpha=\left | -0.00547945205479 \right |+\left |0.00328767123288 \right |\\\\d\alpha=0.00547945205479+0.00328767123288\\\\d\alpha=0.00876712328767\text{ radians}`

Therefore, the maximum error in the calculated value of α is 0.00876712328767 radians.