Question

The area of a rectangular wall of a barn is 126 square feet. It’s length is 4 feet longer than twice it’s width. Find the length and the width of the wall of the barn.

Answer 1

The width is 7 feet and length is 18 feet

Explanation:

Let length of rectangle be "l" and width of rectangle be "w"

The area of a rectangle is length * width

Area is given as 126, so we can write:

`lw=126`

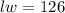
Also, given length is 4 feet longer than TWICE width, so we can write:

l = 4 + 2w

We replace first equation with this equation and simplify to get:

`lw=126\\(4+2w)(w)=126\\4w+2w^2=126\\2w^2+4w-126=0\\w^2+2w-63=0`

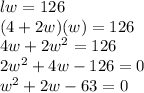
We can do middle term factorization and find the value(s) of w:

`w^2+2w-63=0\\(w+9)(w-7)=0\\w=-9,7`

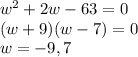
Width CANNOT be negative, so we take w = 7

Now, finding l:

l = 4 + 2w

l = 4 + 2(7)

l = 4 + 14

l = 18

The width is 7 feet and length is 18 feet