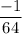Question

Assuming that the equation defines x and y implicitly as differentiable functions xequals​f(t), yequals​g(t), find the slope of the curve xequals​f(t), yequals​g(t) at the given value of t. x cubed plus 4 t squaredequals37​, 2 y cubed minus 2 t squaredequals110​, tequals3

Answer 1

`(dx)/(dt) = -8,(dy)/(dt) = 1/8\\`

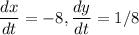
Hence, the slope ,
`(dy)/(dx) = (-1)/(64)`

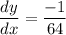
Explanation:

We need to find the slope, i.e.
`(dy)/(dx)`.

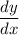and all the functions are in terms of
`t`.

So this looks like a job for the 'chain rule', we can write:

`(dy)/(dx) = (dy)/(dt) .(dt)/(dx) -Eq(A)`

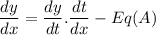
Given the functions

`x = f(t)\\y = g(t)\\`

and

`x^3 +4t^2 = 37 -Eq(B)\\2y^3 - 2t^2 = 110 - Eq(C)`

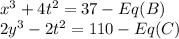
we can differentiate them both w.r.t to
`t`

first we'll derivate Eq(B) to find dx/dt

`x^3 +4t^2 = 37\\3x^2(dx)/(dt) + 8t = 0\\(dx)/(dt) = (-8t)/(3x^2)\\`

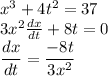
we can also rearrange Eq(B) to find x in terms of t ,
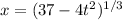`x = (37 - 4t^2)^(1/3)`. This is done so that
`(dx)/(dt)` is only in terms of t.

`(dx)/(dt) = (-8t)/(3(37 - 4t^2)^(2/3))\\`

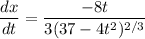
we can find the value of this derivative using t = 3, and plug that value in Eq(A).

`(dx)/(dt) = (-8t)/(3(37 - 4t^2)^(2/3))\\(dx)/(dt) = (-8(3))/(3(37 - 4(3)^2)^(2/3))\\(dx)/(dt) = -8`

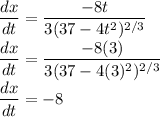
now let's differentiate Eq(C) to find dy/dt

`2y^3 - 2t^2 = 110\\6y^2(dy)/(dt) -4t = 0\\(dy)/(dt) = (4t)/(6y^2)`

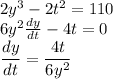
rearrange Eq(C), to find y in terms of t, that is
`y = \left((110 + 2t^2)/(2)\right)^(1/3)`. This is done so that we can replace y in
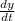`(dy)/(dt)` to make only in terms of t

`(dy)/(dt) = (4t)/(6y^2)\\(dy)/(dt)=(4t)/(6\left((110 + 2t^2)/(2)\right)^(2/3))\\`

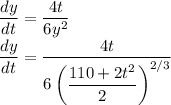
we can find the value of this derivative using t = 3, and plug that value in Eq(A).

`(dy)/(dt) = (4(3))/(6\left((110 + 2(3)^2)/(2)\right)^(2/3))\\(dy)/(dt) = (1)/(8)`

Finally we can plug all of our values in Eq(A)

but remember when plugging in the values that
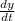`(dy)/(dt)` is being multiplied with
`(dt)/(dx)` and NOT
`(dx)/(dt)`, so we have to use the reciprocal!

`(dy)/(dx) = (dy)/(dt) .(dt)/(dx)\\(dy)/(dx) = (1)/(8).(1)/(-8) \\(dy)/(dx) = (-1)/(64)`

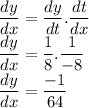
our slope is equal to
`(-1)/(64)`