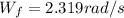Question

A playground merry-go-round has a mass of 115 kg and a radius of 2.50 m and it is rotating with an angular velocity of 0.520 rev/s. The merry-go-round is a solid disk, and the moment of inertia is = 1/2 MR2. . A 23.5 kg child is initially at rest, he then gets onto the merry-go-round by grabbing its outer edge. The child can be treated as a point mass located at the outer edge of the merry-go-round. His moment of inertia is mR2. After this rotational collision, the merry-go-round and the child have a commen final angular velocity (which is different from the merry-go-round's initital angular velocity). (e) What is the final angular velocity in rad/s after the child gets on?

Answer 1

`W_f = 2.319 rad/s`

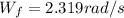
Step-by-step explanation:

For answer this we will use the law of the conservation of the angular momentum.

`L_i = L_f`

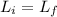
so:

`I_mW_m = I_sW_f`

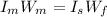
where
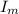`I_m` is the moment of inertia of the merry-go-round,
`W_m` is the initial angular velocity of the merry-go-round,
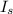`I_s` is the moment of inertia of the merry-go-round and the child together and
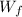`W_f` is the final angular velocity.

First, we will find the moment of inertia of the merry-go-round using:

I =
`(1)/(2)M_mR^2`

I =
`(1)/(2)(115 kg)(2.5m)^2`

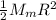
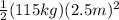
I = 359.375 kg*m^2

Where
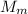`M_m` is the mass and R is the radio of the merry-go-round

Second, we will change the initial angular velocity to rad/s as:

W = 0.520*2
`\pi` rad/s

W = 3.2672 rad/s

Third, we will find the moment of inertia of both after the collision:

`I_s = (1)/(2)M_mR^2+mR^2`

`I_s = (1)/(2)(115kg)(2.5m)^2+(23.5kg)(2.5m)^2`

`I_s = 506.25kg*m^2`

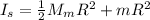
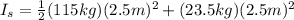
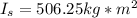
Finally we replace all the data:

`(359.375)(3.2672) = (506.25)W_f`

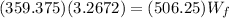
Solving for
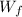`W_f`:

`W_f = 2.319 rad/s`