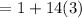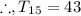Question

Please help mee dont answer if you dunno tho

The graph represents the first three terms in an arithmetic sequence.
a. Find the explicit expression for this sequence
b. Find the recursive expression for this sequence
c What is the 15th term?

Answer 1

A) 1, 4, 7, 11, . . .

B) aₙ = aₙ₋₁ + 3

C) T₁₅ = 43

Explanation:

A) From the graph, we see the points are:
`$ (1,1), (2,4), (3,7) $`.

This means
`$ a = 1 $`

`$ a_2 = a + d = 4 $`

`$a_3 = a + 2d = 7 $`

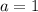
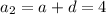
The general term of the arithmetic sequence is:
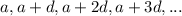`$ a, a+d, a+2d, a+3d, . . . $` where,
`$ a$` is the first term;

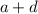`$ a + d $` is the second term and

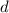`$ d $` is the common difference.

Here, we see that the first term is 1. Second term is 4. Third term is 7. That means each consecutive term is obtained by adding 3 to the previous term. Therefore, according to our assumptions, common difference,
`$ d = 3 $`.

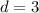B) Recursive formula represents the general form of an arithmetic sequence.

Here, since,
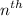`$ n^(th) $` term is obtained by adding 3 to the previous term, the recursive formula would be:
`$ a_n = a_(n - 1) + 3 $`.

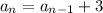C)
`$ 15^(th) $` term:

The formula to calculate
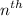`$ n^(th) $` term is:
`$ T_n = a + (n - 1)d $`.

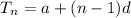Therefore, to find the
`$ 15^(th) $` term, we would have:

`$ T_(15) = 1 + (15 - 1)(3) $`

`$ =1 +  14(3) $`

`$ \therefore, T_(15) = 43 $`