Question

The area of the regular octagon is approximately 54 cm2. A regular octagon has an apothem with length 4 centimeters and an area of 54 centimeters squared. Line segment A B is a side of the octagon. What is the length of line segment AB, rounded to the nearest tenth? a) 3.4 cm b) 4.8 cm c) 24 cm d) 27 cm

Answer 1

the answer is A

Answer 2

The length of line segment AB = 3.4 cm.

Explanation:

Given:

The area of the regular octagon is approximately = 54 cm²

A regular octagon has an apothem with length = 4 cm

AB = side of the octagon

To Find:

AB = side of the octagon = ?

Solution:

A regular octagon has an Eight equal Side

We Know that,

`\textrm{area of regular octagon}=\textrm{Perimeter}* (Apothem)/(2)`

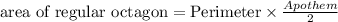
substituting the given values in equation we get

`54 = Perimter* (4)/(2)\\ \\\therefore Perimeter=(54)/(2)\\ \\\therefore Perimeter = 27\ cm\\`

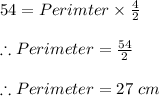
Now,

Perimeter = 8 × Side

∴ Perimeter = 8 × AB

∴ 27 = 8 × AB

∴
`AB =(27)/(8)\\ \\\therefore AB =3.375\ cm\\\\`

After rounded to nearest 10th we get

AB =3.4 cm

The length of line segment AB = 3.4 cm.