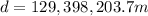Answer:129,398,203.7 m
Step-by-step explanation:
According to Newton's law of Universal Gravitation, the force
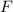 exerted between two bodies of masses
exerted between two bodies of masses
 and
and
 and separated by a distance
and separated by a distance
 is equal to the product of their masses and inversely proportional to the square of the distance:
is equal to the product of their masses and inversely proportional to the square of the distance:
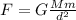 (1)
(1)
Where:
 is the gravitational force
is the gravitational force
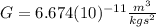 is the gravitational constant
is the gravitational constant
 is the mass of Uranus
is the mass of Uranus
 is the mass of Uranu's moon, Mirana
is the mass of Uranu's moon, Mirana
 is the distance between Uranus and its moon
is the distance between Uranus and its moon
Isolating
 :
:
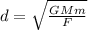 (2)
(2)
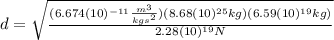 (3)
(3)
Finally: