Question

In a randomly selected sample of 400 registered voters in a community, 160 individuals say that they plan to vote for Candidate Y in the upcoming election. (a) Find the sample proportion planning to vote for Candidate Y. (Round your answer to two decimal places.)

(b) Calculate the standard error of the sample proportion. (Round your answer to three decimal places.)


(c) Find a 95% confidence interval for the proportion of the registered voter population who plan to vote for Candidate Y. (Round your answers to three decimal places.)
to

(d) Find a 98% confidence interval for the proportion of the registered voter population who plan to vote for Candidate Y. (Round your answers to three decimal places.)

Answer 1

a) the sample proportion planning to vote for Candidate Y is
`(160)/(400) =0.4`

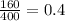
b) the standard error of the sample proportion is ≈ 0.024

c) 95% confidence interval for the proportion of the registered voter population who plan to vote for Candidate Y is (0.353,0.447)

d) 98% confidence interval for the proportion of the registered voter population who plan to vote for Candidate Y is (0.344,0.456)

Explanation:

a) The sample proportion planning to vote for Candidate Y is:

`(160)/(400) =0.4`

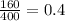
b) The standard error of the sample proportion can be found using

SE=
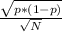`(√(p*(1-p)))/(√(N) )` where

• p is the sample proportion planning to vote for Candidate Y (0.4)

• N is the sample size (400)

Then SE=
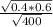`(√(0.4*0.6))/(√(400) )` ≈ 0.024

c) 95% confidence interval for the proportion of the registered voter population who plan to vote for Candidate Y can be calculated as p±z×SE where

• p is the sample proportion planning to vote for Candidate Y (0.4)

• SE is the standard error (0.024)
• z is the statistic for 95% confidence level (1.96)

Then

0.4±(1.96×0.024)=0.4±0.047 that is (0.353,0.447)

d) 98% confidence interval is similarly

0.4±(2.33×0.024)=0.4±0.056 that is (0.344,0.456) where

2.33 is the statistic for 98% confidence level.