Question

A survey found that the American family generates an average of 17.2 pounds of glass garbage trash each year. Assume the standard deviation of the ditribution is 2.5 pounds. Find the probability that the mean of a sample of 47 families will be between 16.6 and 17.6 pounds.

Answer 1

Answer: 0.8137

Explanation:

As per given , we have

`\mu= 17.2\ ,\ \sigma=2.5`

Sample size : n= 47

Let
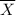`\overline{X}` be the sample mean o.

Then, the probability that the mean of a sample of 47 families will be between 16.6 and 17.6 pounds will be :

`P(16.6<x<17.6)=P((16.6-17.2)/((2.5)/(√(47)))<\frac{\overline{x}-\mu}{(\sigma)/(√(n))}<(17.6-17.2)/((2.5)/(√(47))))`

`=P(-1.645<z<1.097)`

[∵
`z= \frac{\overline{x}-\mu}{(\sigma)/(√(n))}`]

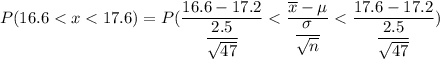
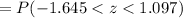
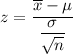`=P(z<1.097)-P(z<-1.645)\\\\=P(z<1.097)-(1-P(z<1.645))\ \ [\because\ P(Z<-z)=1-P(Z<z)]`

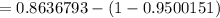`=0.8636793-(1- 0.9500151)` [By using p-value calculator]

`=0.8636793-0.0499849=0.8136944\approx0.8137`

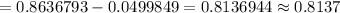
Hence, the probability that the mean of a sample of 47 families will be between 16.6 and 17.6 pounds= 0.8137