Question

The polynomial -x^3-x^2+12x represents the volume of a rectangular aqautic tank in cubic feet. the length of the tank is (x+4).

a . use synthetic division to help you factor the volume of the poly. how many linear factors should you look for?

b. what are the dimensions of the tank?

c. find the value of x that will maximize the volume of the box

d. whats the maximum volume?

Answer 1

a. It should look for 3 linear factors.

b. There are 3 dimensions.

c. x = 1.7

d. Maximum value is 12.597

Explanation:

a.

`-x^(3) - x^(2) + 12 *x` =
`-x^(3) - 4 *x^(2) + 3 *x^(2) +12 *x` =
`-(x + 4) *x^(2) + 3 *x *(x + 4)` =
`(x + 4) *x * (x + 3)`

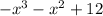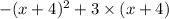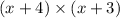
Hence the factorized form of the volume of the poly is
`(x + 4) *x * (x + 3)`

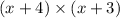
3 linear factors should needed to be look for.

b.

The 3 dimensions are (x + 4), x, (x + 3).

c.

Let, f(x) =
`-x^(3) - x^(2) + 12 *x`

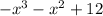
Now,
`(d  f(x))/(dx)` =
`-3 *x^(2) -2 *x + 12`

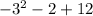
Let
`f1(x)` =
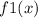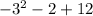`-3 *x^(2) -2 *x + 12` and
`f2(x)` =
`(d f1(x))/(dx)` =
`-3 *x -2`

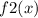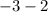
The value will be maximum, if f1(x) = 0 and f2(x) < 0.

`f1(x) = 0`\\
`3 *x^(2) + 2 *x -12 = 0`\\
`x = \frac{- 2 + \sqrt{2^(2) + 4 *3 *12} }{2 *3} , \frac{- 2 - \sqrt{2^(2) + 4 *3 *12} }{2 *3}`

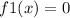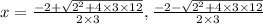
x = 1.69 ≅ 1.7 or x = -2.36 ≅ -2.4

Now f2(1.7) < 0.

At x = 1.7, the volume will be maximum.

d.

The maximum value is f(1.7) = 12.597(approximately)