Answer:
Length of base of triangle = 12 meters
Explanation:
Let the base of the triangle be =
 meters
meters
The height of triangle is 5 less than its base.
So, height of the triangle is given by =

Area of triangle =
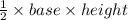
⇒
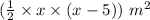
⇒
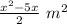 [Using distribution.]
[Using distribution.]
Area of triangle given =
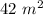
Thus we have:

Multiplying both sides by 2 to remove fraction.
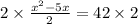
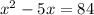
Subtracting both sides by 84.
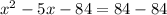
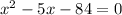
We can now solve quadratic using formula.
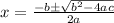
Plugging in values from the quadratic equation to solve for

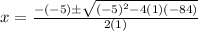
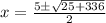
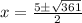
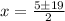
So,
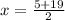 and
and
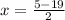
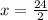 and
and
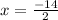
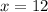 and
and
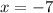
Since length cannot be negative, we take
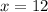 meters as length of base of triangle. (Answer)
meters as length of base of triangle. (Answer)