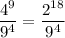Question

What is 4 to the ninth power divided by 9 to the fourth power = 2 to the eighteenth power divided by ____?

Please help, thanks.

Answer 1

`\displaystyle (4^9)/(9^4)=(2^(18))/(9^4)`

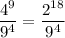
Explanation:

Arithmetic

It's used when We need to deal with the properties and manipulation of numbers, using operations like addition, subtraction, multiplication, and division.

We are given two expressions as part of an identity where one part is missing

`\displaystyle (4^9)/(9^4)=(2^(18))/(?)`

We must use the property of the power of a power

`(x^n)^m=x^(nm)`

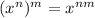
Knowing that
`4=2^2`

`4^9=(2^2)^9=2^(18)`

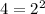
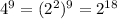
Replacing this value in the identity we have

`\displaystyle (2^(18))/(9^4)=(2^(18))/(?)`

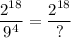
It's evident that the question mark is
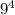`9^4`, so the answer is

`\displaystyle (4^9)/(9^4)=(2^(18))/(9^4)`