Question

A jar contains 4 red marbles and 6 blue marbles. You reach in and randomly select two marbles. If X represents the number of blue marbles you selected, find the expected value of X.

Answer 1

Answer: The required expected value of X is 1.2.

Explanation: Given that a jar contains 4 red marbles and 6 blue marbles. Someone reach in and chose two marbles at random.

We are to find the expected value of X, if X represents the number of blue marbles the person selected.

* X = 0, i.e., two red marbles and 0 blue marbles are selected.

The probability of selecting 0 blue marbles and 2 red marbles is

`P(X=0)=(^4C_2*^6C_0)/(^(10)C_2)=(6*1)/(45)=(2)/(15).`

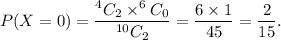
* X = 1, i.e., one red marble and 1 blue marble is selected.

The probability of selecting 1 blue marble and 1 red marble is

`P(X=1)=(^4C_1*^6C_1)/(^(10)C_2)=(4*6)/(45)=(8)/(15).`

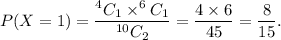
* X = 2, i.e., 0 red marbles and 2 blue marbles are selected.

The probability of selecting 2 blue marbles and 0 red marble is

`P(X=2)=(^4C_0*^6C_2)/(^(10)C_2)=(1*15)/(45)=(1)/(3).`

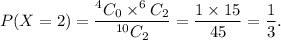
So, the probability distribution of X is given by

`X~~~~~~~~~~~~~~~~~~~~0~~~~~~~~~~~~~~1~~~~~~~~~~~~~~~~~~2\\\\\\P(X)~~~~~~~~~~~~~~(2)/(15)~~~~~~~~~~~~(8)/(15)~~~~~~~~~~~~~~~~~(1)/(3)`

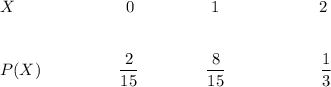
Therefore, the expected value of X is

`E(X)=\sum XP(X)=0*(2)/(15)+1*(8)/(15)+2*(1)/(3)=(18)/(15)=1.2.`

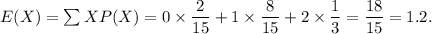
Thus, the required expected value of X is 1.2.