Question

Find the interval(s) where the function is increasing and the interval(s) where it is decreasing. (Enter your answers using interval notation. If the answer cannot be expressed as an interval, enter EMPTY or ∅.) f(x) = 6 − x2 x

Answer 1

f'(x) > 0 on
`(-\infty ,(1)/(e))` and f'(x)<0 on
`((1)/(e),\infty)`

Explanation:

1) To find and interval where any given function is increasing, the first derivative of its function must be greater than zero:

`f'(x)>0`

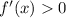
To find its decreasing interval :

`f'(x)<0`

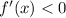
2) Then let's find the critical point of this function:

`f'(x)=\frac{\mathrm{d} }{\mathrm{d} x}[6-2^(2x)]=\frac{\mathrm{d} }{\mathrm{d}x}[6]-\frac{\mathrm{d}}{\mathrm{d}x}[2^(2x)]=0-[ln(2)*2^(2x)*\frac{\mathrm{d}}{\mathrm{d}x}[2x]=-ln(2)*2^(2x)*2=-ln2*2^(2x+1\Rightarrow )f'(x)=-ln(2)*2^(2x)*2\\-ln(2)*2^(2x+1)=-2x^(2x)(ln(x)+1)=0`

2.2 Solving for x this equation, this will lead us to one critical point since x' is not defined for Real set, and x''
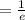`=(1)/(e)`≈0.37 for e≈2.72

`x^(2x)=0 \\i \mathbb{R}\\(ln(x)+1)=0\Rightarrow ln(x)=-1\Rightarrow x=e^(-1)\Rightarrow x\approx 2.72^(-1)x\approx 0.37`

3) Finally, check it out the critical point, i.e. f'(x) >0 and below f'(x)<0.