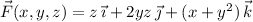
a. The divergence of
 is
is
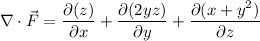

b. The curl of
 is
is
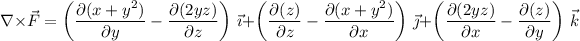
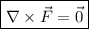
c.
 is conserviatve if there is a scalar function
is conserviatve if there is a scalar function
 for which
for which
 . This means we would need
. This means we would need


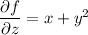
From these conditions we get
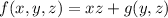
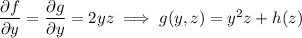

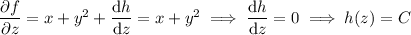
So we do find a potential function
 ,
,
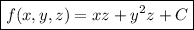
and
 is indeed conservative.
is indeed conservative.
d. Since
 is conservative, and
is conservative, and
 is closed circle, the integral of
is closed circle, the integral of
 along
along
 is 0.
is 0.
e. Since
 is conservative, its integral along
is conservative, its integral along
 depends only on the endpoints. In particular,
depends only on the endpoints. In particular,
