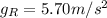Question

If the acceleration due to gravity on the earth is 9.8 m/s2, what is the acceleration due to gravity on Rams? Express your answer in meters per second squared and use two significant figures.

Answer 1

Answer:
`5.70 m/s^(2)`

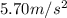
Step-by-step explanation:

This question is incomplete, please remember to post the whole question :)

However, the table related to this question is attached, where it is shown the mass and radius of each planet expressed in terms of Earth's mass
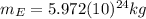`m_(E)=5.972(10)^(24) kg` and Earth's radius
`r_(E)=6371000 m`.

For example, for planet Rams, the mass is
`m_(R)=9.3 m_(E)` and the radius is
`r_(R)=4 r_(E)`.

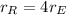Now, for Earth the acceleration due gravity is
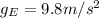`g_(E)=9.8 m/s^(2)` and according to Newton's Universal Law of Gravitation we can find the gravitational forcer exerted by Earth
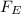`F_(E)` on an object placed on its surface with mass
`m`:

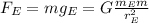`F_(E)=mg_(E)=G(m_(E) m)/(r_(E)^(2))` (1)

Where
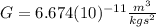`G=6.674(10)^(-11)(m^(3))/(kgs^(2))` is the Gravitational Constant

Simplifying:

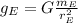`g_(E)=G(m_(E))/(r_(E)^(2))` (2)

Doing the same with planet Rams:

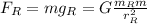`F_(R)=mg_(R)=G(m_(R) m)/(r_(R)^(2))` (3)

Simplifying:

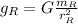`g_(R)=G(m_(R))/(r_(R)^(2))` (4)

Remembering the relation between the Earth's mass and radius with Ram's mass and radius:

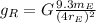`g_(R)=G(9.3 m_(E))/((4r_(E))^(2))` (5)

Solving:

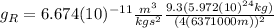`g_(R)=6.674(10)^(-11)(m^(3))/(kgs^(2))(9.3 (5.972(10)^(24) kg))/((4(6371000 m))^(2))` (6)

Finally:

`g_(R)=5.70 m/s^(2)`