Question

Solve the system : x = 2 - y and 3x + 3y = 6

a) ( 4, -2 )

b) ( 1, 1 )

c) Parallel lines

d) Coincident lines

Answer 1

Option is d) Coincident lines.

Explanation:

Given:

x = 2 - y and

3x + 3y = 6

Solution:

Let we rewrite the equations as

x + y = 2 ...................................Equation ( 1 )

3x + 3y = 6 ....................................Equation ( 2 )

Compare the above Two Equations with the following

a₁x + b₁y = c₁ and

a₂x + b₂y = c₂

We get

a₁ = 1 ; b₁ = 1 ; c₁ = 2 and

a₂ = 3 ; b₂ = 3 ; c₂ = 6

Now we will check

`(a_(1))/(a_(2))=(1)/(3)\\\\(b_(1))/(b_(2))=(1)/(3)\\\\(c_(1))/(c_(2))=(2)/(6)=(1)/(3) \\`

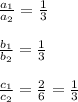
Now we get

`(a_(1))/(a_(2))=(b_(1))/(b_(2))=(c_(1))/(c_(2))=(1)/(3)`

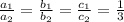
Which is the condition for a COINCIDENT LINES

COINCIDENT LINES have Infinite solutions for different x and different y