Question

The tables represent two linear functions in a system.

A 2 column table with 5 rows. The first column, x, has the entries, negative 6, negative 3, 0, 3. The second column, y, has the entries, negative 22, negative 10, 2, 14. A 2 column table with 5 rows. The first column, x, has the entries, negative 6, negative 3, 0, 3. The second column, y, has the entries, negative 30, negative 21, negative 12, negative 3.
What is the solution to this system?

(negative StartFraction 13 over 3 EndFraction, negative 25)
(negative StartFraction 14 over 3 EndFraction, negative 54)
(–13, –50)
(–14, –54)

Answer 1

(-14,-54)

Explanation:

Answer 2

(-14,-54)

Explanation:

The first function passes through the points (-6,-22), (-3,-10), (0,2) and (3,14).

Now, the equation of the function can be determined from any two points say (0,2) and (3,14).

The equation is
`(y - 14)/(14 - 2) = (x - 3)/(3 - 0)`

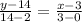
⇒ y - 14 = 4x - 12

⇒ y = 4x + 2 ........... (1)

Now, the second function passes through the points (-6,-30), (-3,-21), (0,-12) and (3,-3).

Now, the equation of the function can be determined from any two points say (0,-12) and (3,-3).

The equation is
`(y + 3)/(-3 - (- 12)) = (x - 3)/(3 - 0)`

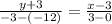
⇒ y + 3 = 3(x - 3)

⇒ y = 3x - 12 ........... (2)

Now, solving equations (1) and (2) we get,

3x - 12 = 4x + 2

⇒ x = - 14

Again, from equation (2), we get

y = 3(- 14) - 12 = - 54

Therefore, the solution is (-14,-54). (Answer)