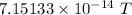Question

During a test, a NATO surveillance radar system, operating at 12 GHz at 190 kW of power, attempts to detect an incoming stealth aircraft at 80 km. Assume that the radar beam is emitted uniformly over a hemisphere. (a) What is the intensity (in ?W/m2) of the beam when the beam reaches the aircraft's location? The aircraft reflects radar waves as though it has a cross-sectional area of only 0.52 m2. (b) What is the power (in mW) of the aircraft's reflection? Assume that the beam is reflected uniformly over a hemisphere. Back at the radar site, what are (c) the intensity, (d) the maximum value of the electric field vector, and (e) the rms value (in ?T) of the magnetic field of the reflected radar beam?

Answer 1

`4.72491\ \mu W/m^2`

`2* 10^(-3)\ mW`

`6.10993* 10^(-13)\ W/m^2`

`2.1454* 10^(-5)\ N/C`

`7.15133* 10^(-14)\ T`

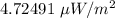
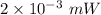
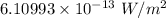
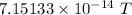
Step-by-step explanation:

A = Area of hemispher =
`2\pi r^2`

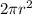
r = Distance

P = Power

I = Intensity

`\epsilon_0` = Permittivity of free space =
`8.85* 10^(-12)\ F/m`

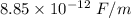
c = Speed of light =
`3* 10^8\ m/s`

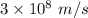
Intensity is given by

`I=(P)/(A)\\\Rightarrow I=(190* 10^3)/(2\pi 80000^2)\\\Rightarrow I=4.72491* 10^(-6)\ W/m^2=4.72491\ \mu W/m^2`

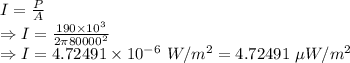
The intensity is
`4.72491\ \mu W/m^2`

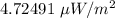
Power is given by

`P=IA\\\Rightarrow P=4.72491* 10^(-6)* 0.52\\\Rightarrow P=2.45695* 10^(-6)=2* 10^(-3)\ mW`

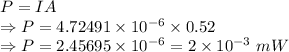
The power is
`2* 10^(-3)\ mW`

`I=(P)/(A)\\\Rightarrow I=(2.45695* 10^(-6))/(2\pi 80000^2)\\\Rightarrow I=6.10993* 10^(-13)\ W/m^2`

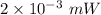
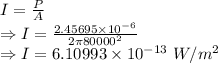
The intensity is
`6.10993* 10^(-13)\ W/m^2`

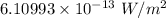
Maximum electric field is given by

`E_0=\sqrt{(2I)/(c\epsilon_0)}\\\Rightarrow E_0=\sqrt{(2* 6.10993* 10^(-13))/(3* 10^8* 8.85* 10^(-12))}\\\Rightarrow E_0=2.1454* 10^(-5)\ N/C`

Maximum value of electric field is
`2.1454* 10^(-5)\ N/C`

Magnetic field is given by

`B=(E_0)/(c)\\\Rightarrow B=(2.1454* 10^(-5))/(3* 10^8)\\\Rightarrow B=7.15133* 10^(-14)\ T`

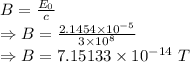
The rms value of magnetic field is
`7.15133* 10^(-14)\ T`