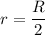Question

A long, straight, cylindrical wire of radius R carries a current uniformly distributed over its cross section. At what location is the magnetic field produced by this current equal to half of its largest value? inside the iwre

Answer 1

`r=(R)/(2)`

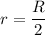
Step-by-step explanation:

We know that maximum value of magnetic field in the long wire

`B_(max)=(\mu _oI)/(2\pi R)`

I=Current ,R=Radius of wire ,B= magnetic field

μo=Constant

At distance r the magnetic filed is the half of the maximum magnetic filed

At distance r

`B=(\mu _oIr)/(2\pi R^2)`

`B=(B_(max))/(2)`

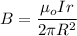
So we can say that

`(\mu _oIr)/(2\pi R^2)=(1)/(2)* (\mu _oI)/(2\pi R)`

`r=(R)/(2)`

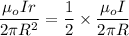
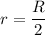
Therefore the answer is
`r=(R)/(2)`