Question

This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to the skipped part.Consider the equation below.f(x) = 2 sin(x) + 2 cos(x), 0 ≤ x ≤ 2πExercise (a)Find the interval on which f is increasing. Find the interval on which f is decreasing.Exercise (b)Find the local minimum and maximum values of f.Exercise (c)Find the inflection points. Find the interval on which f is concave up. Find the interval on which f is concave down.

Answer 1

Explanation:

Given that there is a function of x,

`f(x) = 2sin x + 2cos x,0\leq x\leq 2\pi`

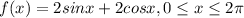
Let us find first and second derivative for f(x)

`f'(x) = 2cosx -2sinx\\f`

When f'(x) =0 we have tanx = 1 and hence

a) f'(x) >0 for I and III quadrant

Hence increasing in
`(0, \pi/2) U(\pi,3\pi/2)\\`

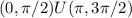
and decreasing in
`(\pi/2, \pi)U(3\pi/2,2\pi)`

`x=(\pi)/(4), (3\pi)/(4)`

`f`

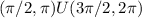
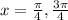
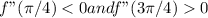
Hence f has a maxima at x = pi/4 and minima at x = 3pi/4

b) Maximum value =
`2sin \pi/4+2cos \pi/4 =2√(2)`

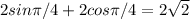
Minimum value =
`2sin 3\pi/4+2cos 3\pi/4 =-2√(2)`

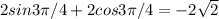
c)

f"(x) =0 gives tanx =-1

`x= 3\pi/4, 7\pi/4`

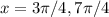
are points of inflection.

concave up in (3pi/4,7pi/4)

and concave down in (0,3pi/4)U(7pi/4,2pi)