Question

If two objects travel through space along two different curves, it's often important to know whether they will collide. (Will a missile hit its moving target? Will two aircraft collide?) The curves might intersect, but we need to know whether the objects are in the same position at the same time. Suppose the trajectories of two particles are given by the vector functions for t 0. Do the particles collide? If they collide find t. If not enter NONE.r1(t)=r2(t)=<9t-14,t^2,13t-42>t=

Answer 1

The particles collide when t = 7 at the point (49, 49, 49).

Explanation:

We know the trajectories of the two particles,

`r_1(t)=\langle t^2,16t-63,t^2\rangle\\r_2(t)=\langle 9t-14,t^2,13t-42\rangle`

To find if the tow particles collide you must:

• Equate the x-components for each particle and solve for t

`t^2=9t-14\\t^2-9t+14=0\\\left(t^2-2t\right)+\left(-7t+14\right)=0\\t\left(t-2\right)-7\left(t-2\right)=0\\\left(t-2\right)\left(t-7\right)=0`

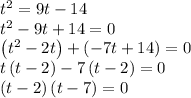
The solutions to the quadratic equation are:

`t=2,\:t=7`

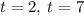
• Equate the y-components for each particle and solve for t

`16t-63=t^2\\^2-16t+63=0\\\left(t^2-7t\right)+\left(-9t+63\right)=0\\t\left(t-7\right)-9\left(t-7\right)=0\\\left(t-7\right)\left(t-9\right)=0`

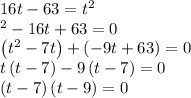
The solutions to the quadratic equation are:

`t=7,\:t=9`

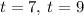
• Equate the z-components for each particle and solve for t

`t^2=13t-42\\t^2-13t+42=0\\\left(t^2-6t\right)+\left(-7t+42\right)=0\\t\left(t-6\right)-7\left(t-6\right)=0\\\left(t-6\right)\left(t-7\right)=0`

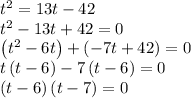
The solutions to the quadratic equation are:

`t=6,\:t=7`

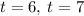
Evaluate the position vectors at the common time. The common solution is when t = 7.

`r_1(7)=\langle 7^2,16(7)-63,7^2\rangle=\langle 49,49,49\rangle\\\\r_2(7)=\langle 9(7)-14,7^2,13(7)-42\rangle=\langle 49,49,49\rangle`

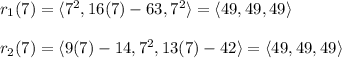
For two particles to collide, they must be at exactly the same coordinates at exactly the same time.

The particles collide when t = 7 at the point (49, 49, 49).