Question

USA Today reported that about 47% of the general consumer population in the United States is loyal to the automobile manufacturer of their choice. Suppose Chevrolet did a study of a random sample of 1006 Chevrolet owners and found that 490 said they would buy another Chevrolet. Does this indicate that the population proportion of consumers loyal to Chevrolet is more than 47%? Use alpha = 0.01.

Answer 1

Answer: No, It does not indicates that the population proportion of consumers loyal to Chevrolet is more than 47%.

Explanation:

Let p denotes the proportion of consumers loyal to Chevrolet.

As per given , we have

`H_0: p=0.47\\\\ H_a: p>0.47`

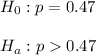
Since the alternative hypothesis
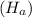`(H_a)` is right-tailed so the test would be a right-tailed test.

Also , it is given that ,Chevrolet did a study of a random sample of 1006 Chevrolet owners and found that 490 said they would buy another Chevrolet.

i.e. n = 1006

x= 490

`\hat{p}=(490)/(1006)=0.487`

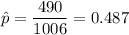
Test statistic :

`z=\frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

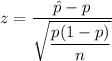
, where p=population proportion.

`\hat{p}`= sample proportion

n= sample size.

i.e.
`z=\frac{0.487-0.47}{\sqrt{(0.47(1-0.47))/(1006)}}=1.08`

P-value (for right-tailed test)= P(z>1.08)=1-P(z≤1.08) [∵P(Z>z)=1-P(Z≤z)]

=1- 0.8599=0.1401 [By z-value table.]

Decision : Since p-value (0.14) is greater than the significance level (
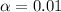`\alpha=0.01`) , it means we are failed to reject the null hypothesis.

Conclusion : We have sufficient evidence to support the claim that about 47% of the general consumer population in the United States is loyal to the automobile manufacturer of their choice.

Hence, it does not indicates that the population proportion of consumers loyal to Chevrolet is more than 47%.