Question

A 191 191 kg sculpture hangs from a horizontal rod that serves as a pivot about which the sculpture can oscillate. The sculpture's moment of inertia with respect to the pivot is 17.2 17.2 kg·m2, and when it is swung at small amplitudes, it is found to oscillate at a frequency of 0.925 0.925 Hz. How far is the pivot from the sculpture's center of mass?

Answer 1

r = 0.31 m

Step-by-step explanation:

Given that,

Mass of the sculpture, m = 191 kg

The sculpture's moment of inertia with respect to the pivot is,
`I=17.2\ kg-m^2`

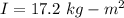
Frequency of oscillation, f = 0.925 Hz

Let r is the distance of the the pivot from the sculpture's center of mass. The frequency of oscillation is given by :

`f=(1)/(2\pi)\sqrt{(mgr)/(I)}`

`r=(4\pi^2f^2I)/(mg)`

`r=(4\pi^2* 0.925^2* 17.2)/(191* 9.8)`

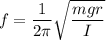
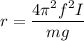
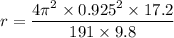
r = 0.31 m

So, the pivot is 0.31 meters from the sculpture's center of mass. Hence, this is the required solution.