Question

Blood takes about 1.45 s 1.45 s to pass through a 2.00 mm 2.00 mm long capillary. If the diameter of the capillary is 5.00 μm 5.00 μm and the pressure drop is 2.35 kPa , 2.35 kPa, calculate the viscosity of blood. Assume laminar flow.

Answer 1

266.21 Pa.s

Step-by-step explanation:

By Hagen–Poiseuille equation,

ΔP = 128 μ LQ/ πd2

Where;

Δp is the pressure difference between the two ends,

L is the length,

μ is the dynamic viscosity,

Q is the volumetric flow rate,

d = diameter

t = is the time

Δp = 2.35 KPa = 2.350Pa

L= 2.00 mm = 0.002m

μ = ??? (unknown)

Q = V × A

= (L/t) A

= Lπ
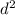`d^(2)`/ 4t ( since A =
`d^(2)`)

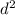d= 5.00 μm = 5.00 × 10 -6

t = 1.45s

∴ 2350 = (128 μ L/ π
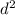`d^(2)` ) × (L π
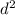`d^(2)` / 4t)

Q(volumetric flow rate) = 32μ
`L^(2)` /
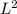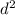`d^(2)`t

From ΔP = 128 μ LQ/ π
`d^(2)`

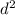
μ = ΔP π
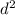`d^(2)` / LQ

= (2350
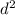`d^(2)` / t) / 32L2

= [2350 × (5.00 × 10 -6 ) ( 1.45) / 32( 0.002)2]

= [(0.034075/ (32 × 0.000004)]

= 0.034075/ 0.000128

= 266.21 Pa.s