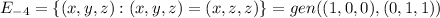Question

(1 point) The matrix A=⎡⎣⎢−4−4−40−8−4084⎤⎦⎥A=[−400−4−88−4−44] has two real eigenvalues, one of multiplicity 11 and one of multiplicity 22. Find the eigenvalues and a basis of each eigenspace. λ1λ1 = equation editorEquation Editor has multiplicity 11, with a basis of equation editorEquation Editor . λ2λ2 = equation editorEquation Editor has multiplicity 22, with a basis of equation editorEquation Editor .

Answer 1

We have the matrix
`A=\left[\begin{array}{ccc}-4&-4&-4\\0&-8&-4\\0&8&4\end{array}\right]`

To find the eigenvalues of A we need find the zeros of the polynomial characteristic
`p(\lambda)=det(A-\lambda I_3)`

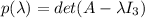
Then

`p(\lambda)=det(\left[\begin{array}{ccc}-4-\lambda&-4&-4\\0&-8-\lambda&-4\\0&8&4-\lambda\end{array}\right] )\\=(-4-\lambda)det(\left[\begin{array}{cc}-8-\lambda&-4\\8&4-\lambda\end{array}\right] )\\=(-4-\lambda)((-8-\lambda)(4-\lambda)+32)\\=-\lambda^3-8\lambda^2-16\lambda`

Now, we fin the zeros of
`p(\lambda)`.

`p(\lambda)=-\lambda^3-8\lambda^2-16\lambda=0\\\lambda(-\lambda^2-8\lambda-16)=0\\\lambda_(1)=0\; o \; \lambda_(2,3)=(8\pm√(8^2-4(-1)(-16)))/(-2)=(8)/(-2)=-4`

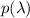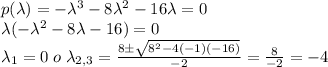
Then, the eigenvalues of A are
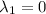`\lambda_(1)=0` of multiplicity 1 and
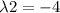`\lambda{2}=-4` of multiplicity 2.

Let's find the eigenspaces of A. For
`\lambda_(1)=0`:
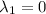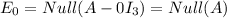`E_0 = Null(A- 0I_3)=Null(A)`.Then, we use row operations to find the echelon form of the matrix

`A=\left[\begin{array}{ccc}-4&-4&-4\\0&-8&-4\\0&8&4\end{array}\right]\rightarrow\left[\begin{array}{ccc}-4&-4&-4\\0&-8&-4\\0&0&0\end{array}\right]`

We use backward substitution and we obtain

1.

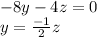
`-8y-4z=0\\y=(-1)/(2)z`

2.

`-4x-4y-4z=0\\-4x-4((-1)/(2)z)-4z=0\\x=(-1)/(2)z`

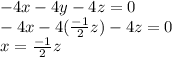
Therefore,

`E_0=\{(x,y,z): (x,y,z)=(-(1)/(2)t,-(1)/(2)t,t)\}=gen((-(1)/(2),-(1)/(2),1))`

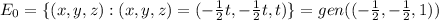
For
`\lambda_(2)=-4`:
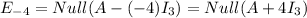`E_(-4) = Null(A- (-4)I_3)=Null(A+4I_3)`.Then, we use row operations to find the echelon form of the matrix

`A+4I_3=\left[\begin{array}{ccc}0&-4&-4\\0&-4&-4\\0&8&8\end{array}\right] \rightarrow\left[\begin{array}{ccc}0&-4&-4\\0&0&0\\0&0&0\end{array}\right]`

We use backward substitution and we obtain

1.

`-4y-4z=0\\y=-z`

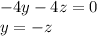
Then,

`E_(-4)=\{(x,y,z): (x,y,z)=(x,z,z)\}=gen((1,0,0),(0,1,1))`