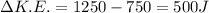Answer:
Step-by-step explanation:
Given
mass of body A
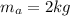
mass of body
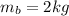
Velocity before Collision is

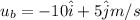
after collision

let
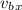 and
and
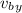 velocity of B after collision in x and y direction
velocity of B after collision in x and y direction
conserving momentum in x direction

as
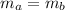 thus
thus
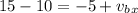
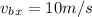
Conserving momentum in Y direction
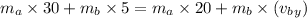
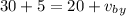

thus velocity of B after collision is
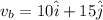
(b)Change in total Kinetic Energy
Initial Kinetic Energy of A And B
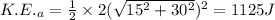
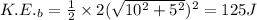
Total initial Kinetic Energy =1250 J
Final Kinetic Energy of A And B
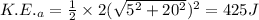
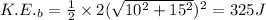
Final Kinetic Energy
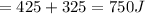
Change