Answer:
(a) and (b) see pictures attached
(c) V = 16/35
Explanation:
(a) Sketch the base of S in the xy-plane.
See picture 1 attached
(b) Sketch a three-dimensional picture of S with the xy-plane as the floor.
See picture 2 attached
(c) Compute the volume of S.
The volume is given by the triple integral

The cross-sections perpendicular to the x-axis are squares so
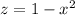
The region S is given by the following inequalities
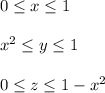
Therefore
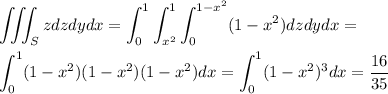
So the volume V of the solid S is
V=16/35