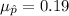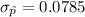Question

The proportion of students at a college who have GPA higher than 3.5 is 19%. a. You take repeated random samples of size 25 from that college and find the proportion of student who have GPA higher than 3.5 for each sample. What is the mean and the standard error of the sampling distribution of the sample proportions?

Answer 1

`\mu_{\hat{p}}=0.19`

`\sigma_{\hat{p}}=0.0785`

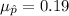
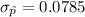
Explanation:

We know that the mean and the standard error of the sampling distribution of the sample proportions will be :-

`\mu_{\hat{p}}=p`

`\sigma_{\hat{p}}=\sqrt{(p(1-p))/(n)}`

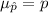
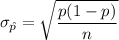
, where p=population proportion and n= sample size.

Given : The proportion of students at a college who have GPA higher than 3.5 is 19%.

i.e. p= 19%=0.19

The for sample size n= 25

The mean and the standard error of the sampling distribution of the sample proportions will be :-

`\mu_{\hat{p}}=0.19`

`\sigma_{\hat{p}}=\sqrt{(0.19(1-0.19))/(25)}\\\\=√(0.006156)=0.0784601809837\approx0.0785`

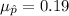
Hence , the mean and the standard error of the sampling distribution of the sample proportions :

`\mu_{\hat{p}}=0.19`

`\sigma_{\hat{p}}=0.0785`