Question

Given: g(x) = 2x2 + 3x + 10

k(x) = 2x+16
Solve the equation g(x) = 2x(x) algebraically for x, to the nearest tenth. Explain why you
shose the method you used to solve this quadratic equation.​

Answer 1

x = 3.576 and x = - 3.076

Explanation:

Two functions are given to be, g(x) = 2x² + 3x + 10 and k(x) = 2x + 16.

Now, we have to solve the equation g(x) = 2k(x)

⇒ 2x² + 3x + 10 = 4x + 32

⇒2x² - x - 22 = 0

The expression in the left hand side can not be factorized and therefore we have to use Sridhar Acharya formula which gives the solutions of the equation in the form ax² + bx + c = 0 are given by

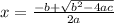`x = \frac{-b + \sqrt{b^(2) - 4ac} }{2a}` and
`x = \frac{-b - \sqrt{b^(2) - 4ac} }{2a}`

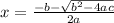
Therefore, the solutions of the given equation are

`x = \frac{-(- 1) + \sqrt{(- 1)^(2) - 4 (2)(-22)}  }{2(2)} = 3.576`

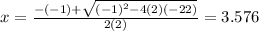
and
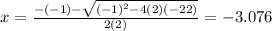`x = \frac{-(- 1) - \sqrt{(- 1)^(2) - 4 (2)(-22)}  }{2(2)} = -3.076` (Answer)