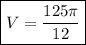Question

use the general slicing method to find the volume of The solid whose base is the triangle with vertices (0 comma 0 )​, (15 comma 0 )​, and (0 comma 15 )and whose cross sections perpendicular to the base and parallel to the​ y-axis are semicircles

Answer 1

volume V of the solid

`\boxed{V=\displaystyle(125\pi)/(12)}`

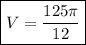
Explanation:

The situation is depicted in the picture attached

(see picture)

First, we divide the segment [0, 5] on the X-axis into n equal parts of length 5/n each

[0, 5/n], [5/n, 2(5/n)], [2(5/n), 3(5/n)],..., [(n-1)(5/n), 5]

Now, we slice our solid into n slices.

Each slice is a quarter of cylinder 5/n thick and has a radius of

-k(5/n) + 5 for each k = 1,2,..., n (see picture)

So the volume of each slice is

`\displaystyle(\pi(-k(5/n) + 5 )^2*(5/n))/(4)`

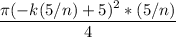
for k=1,2,..., n

We then add up the volumes of all these slices

`\displaystyle(\pi(-(5/n) + 5 )^2*(5/n))/(4)+\displaystyle(\pi(-2(5/n) + 5 )^2*(5/n))/(4)+...+\displaystyle(\pi(-n(5/n) + 5 )^2*(5/n))/(4)`

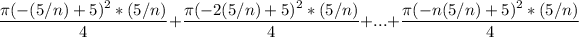
Notice that the last term of the sum vanishes. After making up the expression a little, we get

`\displaystyle(5\pi)/(4n)\left[(-(5/n)+5)^2+(-2(5/n)+5)^2+...+(-(n-1)(5/n)+5)^2\right]=\\\\\displaystyle(5\pi)/(4n)\displaystyle\sum_(k=1)^(n-1)(-k(5/n)+5)^2`

But

`\displaystyle(5\pi)/(4n)\displaystyle\sum_(k=1)^(n-1)(-k(5/n)+5)^2=\displaystyle(5\pi)/(4n)\displaystyle\sum_(k=1)^(n-1)((5/n)^2k^2-(50/n)k+25)=\\\\\displaystyle(5\pi)/(4n)\left((5/n)^2\displaystyle\sum_(k=1)^(n-1)k^2-(50/n)\displaystyle\sum_(k=1)^(n-1)k+25(n-1)\right)`

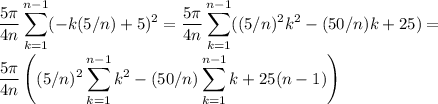
we also know that

`\displaystyle\sum_(k=1)^(n-1)k^2=\displaystyle(n(n-1)(2n-1))/(6)`

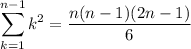
and

`\displaystyle\sum_(k=1)^(n-1)k=\displaystyle(n(n-1))/(2)`

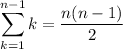
so we have, after replacing and simplifying, the sum of the slices equals

`\displaystyle(5\pi)/(4n)\left((5/n)^2\displaystyle\sum_(k=1)^(n-1)k^2-(50/n)\displaystyle\sum_(k=1)^(n-1)k+25(n-1)\right)=\\\\=\displaystyle(5\pi)/(4n)\left(\displaystyle(25)/(n^2).\displaystyle(n(n-1)(2n-1))/(6)-\displaystyle(50)/(n).\displaystyle(n(n-1))/(2)+25(n-1)\right)=\\\\=\displaystyle(125\pi)/(24).\displaystyle(n(n-1)(2n-1))/(n^3)`

Now we take the limit when n tends to infinite (the slices get thinner and thinner)

`\displaystyle(125\pi)/(24)\displaystyle\lim_(n \rightarrow \infty)\displaystyle(n(n-1)(2n-1))/(n^3)=\displaystyle(125\pi)/(24)\displaystyle\lim_(n \rightarrow \infty)(2-3/n+1/n^2)=\\\\=\displaystyle(125\pi)/(24).2=\displaystyle(125\pi)/(12)`

and the volume V of our solid is

`\boxed{V=\displaystyle(125\pi)/(12)}`