Question

A bullet of mass m = 40~\text{g}m=40 g, moving horizontally with speed vv, strikes a clay block of mass M = 1.35M=1.35 kg that is hanging on a light inextensible string of length L = 0.753L=0.753. The bullet becomes embedded in the block, which was originally at rest. What is the smallest value of vv which would cause the block-on-a-string to swing around and execute a complete vertical circle?

Answer 1

v > 133.5 m/s

Step-by-step explanation:

Let's analyze this problem a little, park run a complete circle we must know the speed of the system at the top of the circle.

Let's start by using the concepts of energy to find the velocity at the top of the circle

Initial. Top circle

Em₀ = K + U = ½ m v² + m g y

If we place the reference system at the bottom of the cycle y = 2R = L

Em₀ = ½ m v² + m g y

final. Low circle

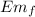`Em_(f)` = K = ½ m v₁²

Emo =
`Em_(f)`

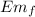
½ m v² + m g y = 1/2 m v₁²

v₁² = v² + (2g L)

v₁² = v² + 2 g L

The smallest value that v can have is zero, with this value the bullet + block system reaches this point and falls, with any other value exceeding it and completing the circle. Let's calculate for this minimum speed point

v₁ = √2g L

We already have the speed system at the bottom we can use the moment

Starting point before crashing

p₀ = m v₀

End point after collision at the bottom of the circle

`p_(f)` = (m + M) v₁

The system is formed by the two bodies and therefore the forces to last before the crash are internal and the moment is conserved

p₀ =
`p_(f)`

m v₀ = (m + M) v₁

v₀ = (m + M) / m v₁

Let's replace

v₀ = (1+ M / m) √ 2g L

Let's reduce to the SI system

m = 40 g (kg / 1000g) = 0.040 kg

Let's calculate

v₀ = (1 + 1.35 / 0.040) RA (2 9.8 0.753)

v₀ = 34.75 3.8417

v₀ = 133.5 m / s

the velocity must be greater than this value

v > 133.5 m/s