Question

48000 fair dice are rolled independently. Let X count the number of sixes that appear. (a) What type of random variable is X? (b) Write the expression for the probability that between 7500 and 8500 sixes show. That is Pp7500 ď X ď 8500q. (c) The sum you wrote in part b) is ridiculous to evaluate. Instead, approximate the value by a normal distribution and evaluate in terms of the distribution Φpxq " PpNp0, 1q ď xq of a standard normal random variable. (d) Why do you think a normal distribution is a good choice for approximation

Answer 1

1 because almost certain event

Explanation:

whenever a fair die is rolled the number of getting a 6 is having probability 1/6. Each throw is independent of the other

Hence no of sixes would be binomial with p=1/6

when 48000 dice are rolled, using binomial would be a hectic task.

Hence we approximate to normal distribution

X - no of sixes in 48000 throws would be normal

with mean = np = 8000

Var =npq = 6666.667

Std dev = 81.650

Now it is easier to find out

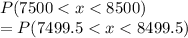`P(7500<x<8500)\\=P(7499.5<x<8499.5)`(using continuity correctin)

=
`P(|z|<6.1295)\\=1`

we get this probability almost equal to 1

d) Normal distribution is a good choice because when no of trials increase using binomial and combination formulae would not be easy