Question

Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1800 kg and was approaching at 5.00 m/s due south. The second car has a mass of 700 kg and was approaching at 21.0 m/s due west. (a) Calculate the final velocity of the cars. (b) How much kinetic energy is lost in the collision? (This energy goes into deformation of the cars.)

Answer 1

The final velocity of the cars is 6.894 m/s

The kinetic energy lost is 117,441 J

Step-by-step explanation:

Using the conservation of the linear momentum :

`P_i = P_f`

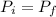
Where
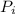`P_i` is the inicial linear momentum and
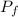`P_f` is the final linear momemtum.

The linear momentum is calculated by:

`P = MV`

where M is the mass and V is the velocity.

First we identify the directions of the velocity of both cars:

• the first car is moving in the axis y for the south direction, we will take this direction like positive.
• the second car is moving in the axis x to the west, we will take this direction like positive.

The conservation of the linear momentum is made on direction x, so:

`P_i = P_f\\M_(1)V_(1ix) +M_(2)V_(2ix) = V_(sx)(M_1+M_2)`

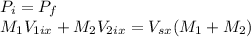
where
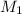`M_1` is the mass of the car 1,
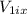`V_(1ix)` is the car 1's inicial velocity in the axis x,
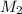`M_2` is the mass of the car 2,
`V_(2ix)` is the car 2's inicial velocity in the axis x and
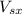`V_(sx)` is the velocity of the car 1 and car 2 after the collition.

The car 1 just move in the axis y so, it dont have horizontal velocity (
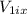`V_(1ix)` = 0)

now the equation is:

`M_2V_(2ix) = V_(sx)(M_1 +M_2)`

Replacing the values, we get:

(700 kg)(21 m/s) =
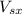`V_(sx)`( 1800 kg + 700 kg)

solving for
`V_(sx)`:

`V_(sx) = (700(21))/(1800+700)`

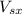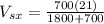
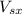`V_(sx)` = 5.88 m/s

Now we do the conservation of the linear momentum on direction y:

`P_i = P_f\\M_(1)V_(1iy) +M_(2)V_(2iy) = V_(sy)(M_1+M_2)`

where
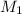`M_1` is the mass of the car 1,
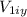`V_(1iy)` is the car 1's inicial velocity in the axis y,
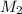`M_2` is the mass of the car 2,
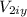`V_(2iy)` is the car 2's inicial velocity in the axis y and
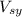`V_(sy)` is the velocity of the car 1 and car 2 together after the collition.

The car 2 just move in the axis x so, it don't have horizontal velocity (
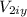`V_(2iy)` = 0)

now the equation is:

`M_1V_(1iy) = V_(sy)(M_1 +M_2)`

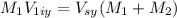
Replacing the values, we get:

`1800(5 m/s) = V_(sy)(1800 +700)`

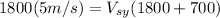
solving for
`V_(sx)`:

`V_(sy) = (1800(5))/(1800+700)`

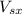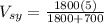
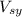`V_(sy)` = 3.6 m/s

Now, we have the two components of the velocity and using pythagorean theorem we find the answer as:

`V_f = √(5.88^2+3.6^2)`

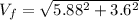
`V_f =` 6.894 m/s

Finally we have to find the kinetic energy lost, so the kinetic energy is calculated by:

K =
`(1)/(2)MV^2`

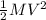
so, ΔK =
`K_f -K_i`

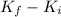
where
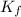`K_f` is the final kinetic energy and
`K_i` is the inicial kinetic energy.

then:

`K_i = (1)/(2)(1800)(5)^2+(1)/(2)(700)(21)^2= 176,850 J`

`K_f = (1)/(2)(1800+700)(6.894)^2 = 59,409 J`

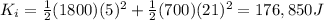
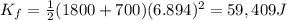
so:

ΔK = 59409 - 176850 = -117441 J