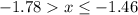Question

−9x+2>18 OR 13x+15≤−4

Answer 1

`-1.78>x\leq -1.46`

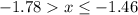
Explanation:

1. Understanding the type of statement

We are given an OR statement. A certain x-value is a set of solution of the statement if it satisfies both of the inequalities.

Therefore, the solution of this statement is the Union of set of the solutions of both inequalities.

2. Finding the solutions to the two inequalities

`-9x+2>18\\-9x>18-2\\-9x>16\\x<-(16)/(9)\\ \\x<-1.78`

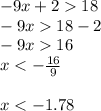
Now Solving for other equation we get,

`13x+15\leq-4\\13x\leq -4-15\\13x\leq -19\\x\leq -(19)/(13)\\ \\x\leq -1.46`

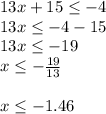
3. The solution is:

`-1.78>x\leq -1.46`

Answer 2

`x \leq - 1.462`

Explanation:

Let solve each inequation:

`-9\cdot x + 2 > 18`

`-16 > 9\cdot x`

`9\cdot x < - 16`

`x < - (16)/(9)`

`x < -1.778`

`13\cdot x + 15 \leq -4`

`13\cdot x \leq -19`

`x \leq -(19)/(13)`

`x \leq -1.462`

The boolean operator OR means that proposition is true if at least one equation is true. Then, the domain that fulfill the proposition is:

`x \leq - 1.462`