Question

For a rectangular cube with a square base, suppose that it costs $3/cm^2 for the material used on the side and $6/cm^2 for the material used for the top lid and the base. Assuming that the volume of this container is 54 cm^3 , what is the side length of the cube with the smallest cost?

Answer 1

The sides of the container should be 3 cm and height should be 6 cm to minimize the cost

Explanation:

Data provided in the question:

costs for the material used on the side = $3/cm²

costs for the material used for the top lid and the base = $6/cm²

Volume of the container = 54 cm³

Now,

let the side of the base be 'x' and the height of the box be 'y'

Thus,

x × x × y = 54 cm³

or

x²y = 54

or

y =
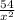`(54)/(x^2)` ............(1)

Now,

The total cost of material, C

C = $3 × ( 4 side area of the box ) + $6 × (Area of the top and bottom)

or

C = ( $3 × 4xy ) + ( $6 × (x²) )

substituting the value of y in the above equation, we get

C =
`3x*4*(54)/(x^2)+2*6x^2`

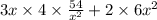
or

C =
`(648)/(x)+12x^2`

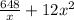
Differentiating with respect to x and putting it equals to zero to find the point of maxima of minima

thus,

C' =
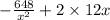`-(648)/(x^2)+2*12x` = 0

or

`2*12x=(648)/(x^2)`

or

24x³ = 648

or

x = 3 cm

also,

C'' =
`+(2*648)/(x^3)+2*12`

or

C''(3) =
`+(2*648)/(3^3)+2*12` > 0

Hence,

x = 3 cm is point of minima

Therefore,

y =
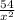`(54)/(x^2)` [from 1]

or

y =
`(54)/(3^2)`

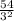
or

y = 6 cm

Hence,

The sides of the container should be 3 cm and height should be 6 cm to minimize the cost