Answer:
p=0.063
Explanation:
Let X be number of the certain brand of jelly beans that are made so that each package contains about the same number of beans.
X is N(375, 8)
YOu are collecting a sample size of
n = 8
Findings from the sample
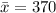
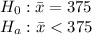
(Left tailed test at 5% level)
Since sample size is small though sigma is known we use Z test, since norm
Mean difference = -5
Std error =
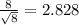
Test statistic t = mean diference / std error =
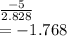
df = n-1 =5
p value = 0.063