Question

A process is measuring the number of returns per 100 receipts at a local retail store. The number of returns were 10, 9, 11, 7, 3, 12, 8, 4, 6, 11. Find the standard deviation of this sampling distribution.

Answer 1

The standard deviation of this sampling distribution is 3.07

Step-by-step explanation:

There are n = 10 samples

Mean:
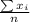`(\sum x_(i))/(n)` = (10 + 9 + 11 + 7 + 3 + 12 + 8 + 4 + 6 + 11) / 10 = 8.1

Variance: s^2 =
`\frac{\sum {(x_(i) - mean)^(2)}}{n-1}`

= [(10 - 8.1)^2 + (9 - 8.1)^2 + (11 - 8.1)^2 + (7 - 8.1)^2+ (3 - 8.1)^2+ (12 - 8.1)^2] + (8 - 8.1)^2+ (4 - 8.1)^2+ (6 - 8.1)^2+ (11 - 8.1)^2] / 9

= 9.43

Standard deviation: s =
`√(s^2)` =
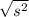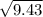`√(9.43)` = 3.07