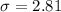Answer:
Mean :
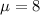
Variance :

Standard deviation =
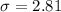
Explanation:
We know that , in Binary Distribution having parameters p (probability of getting success in each trial) and n (Total number trials) , the mean and variance is given by:-
Mean :
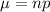
Variance :

We are given that ,
Total social security recipients : n=800
The probability of social security recipients are too young to vote : p=1%= 0.01
Here success is getting social security recipients are too young to vote .
Then, the mean, variance and standard deviation of the number of recipients who are too young to vote will be :-
Mean :

Variance :
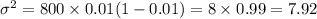
Standard deviation =
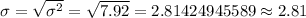
Hence, the mean, variance and standard deviation of the number of recipients who are too young to vote :
Mean :
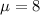
Variance :

Standard deviation =