AB = 3 + x DC = 4x AD = y + 1 BC = 2y Quadrilateral ABCD is a parallelogram if both pairs of opposite sides are congruent. Show that quadrilateral ABCD is a parallelogram by fin…

Question

asked Nov 16, 2020 130k views

1 Answer

Polyglot · Answer 1 · 2020-11-20T13:38:23+0000

Answer:

Option A) 4, 2

Explanation:

We are given that quadrilateral ABCD is a parallelogram with sides:

$AB = 3 + x\\DC = 4x\\AD = y + 1\\BC = 2y$

Since the opposite sides of a parallelogram are equal, we can write:

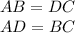
$AB = DC\\AD=BC$

Equating the sides we get,

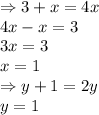
$\Rightarrow 3+x = 4x\\4x-x = 3\\3x = 3\\x = 1\\\Rightarrow y + 1 = 2y\\y = 1$

Putting the values of x and y, we get:

$AB = 3 + x =4\\DC = 4x =4\\AD = y + 1=2\\BC = 2y=2$

Thus, the lengths of the opposite side pairs is 4,2.