Question

An airplane is flying at 300 mi/h at 4000 m standard altitude. As is typical, the air velocity relative to the upper surface of the wing, near its maximum thickness, is 26 percent higher than the plane’s velocity. Using Bernoulli’s equation, calculate the absolute pressure at this point on the wing. Neglect elevation changes and compressibility.

Answer 1

57330.17766 Pa

Step-by-step explanation:

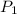`P_1` = Pressure at 4000 m = 61660 Pa

`\rho` = Density at 4000 m = 0.8194 kg/m³

(Values taken from table of properties of air)

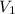`V_1` = Velocity of jet =
`300* (1609.34)/(3600)=134.11\ m/s`

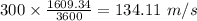
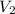`V_2` = Velocity at max thickness

`V_2=1.26V_1=1.26* 134.11=168.9786\ m/s`

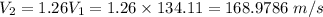
From Bernoulli's equation

`P_1+(1)/(2)\rho V_1^2=P_2+(1)/(2)\rho V_2^2\\\Rightarrow P_2=P_1+(1)/(2)\rho V_1^2-(1)/(2)\rho V_2^2\\\Rightarrow P_2=61660+(1)/(2)* 0.8194* 134.11^2-(1)/(2)* 0.8194* 168.9786^2\\\Rightarrow P_2=57330.17766\ Pa`

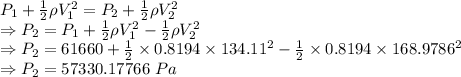
The absolute pressure at this point on the wing is 57330.17766 Pa