Question

A book contains 400 pages. If their are 80 typing errors randomly distributed throughout the book, use the Poisson distribution to determine the probability that a page contains exactly 2 errors

Answer 1

Using the Poisson distribution to determine the probability that a page contains exactly 2 errors is 0.0163

Solution:

Given that, a book contains 400 pages.

There are 80 typing errors randomly distributed throughout the book,

We have to use the Poisson distribution to determine the probability that a page contains exactly 2 errors.

The Poisson distribution formula is given as:

`\text { Probability distribution }=e^(-\lambda) (\lambda^(k))/(k !)`

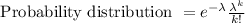
Where,
`\lambda` is event rate of distribution. For observing k events.

`\text { Here rate of distribution } \lambda=\frac{\text { go mistakes }}{400 \text { pages }}=(1)/(5)`

And, k = 2 errors.

`\begin{array}{l}{\text { Then, } \mathrm{p}(2)=e^{-(1)/(5)} * ((1)/(5))/(2 !)} \\\\ {=2.7^{-(1)/(5)} * ((1)/(5^(2)))/(2 * 1)} \\\\ {=\frac{1}{2.7^{(1)/(5)}} * ((1)/(25))/(2)}\end{array}`

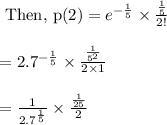
`\begin{array}{l}{=\frac{1}{\sqrt[5]{2.7}} * (1)/(25) * (1)/(2)} \\\\ {=\frac{1}{50 \sqrt[5]{2.7}}} \\\\ {=0.0163}\end{array}`

Hence, the probability is 0.0163