Question

Does anyone know the answer for the question below.

Answer 1

B. (1, 0)

Explanation:

Given:

The two functions are:

`f(x)=\ln(x)\\g(x)=\ln (x^2)`

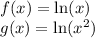
In order to determine the point of intersection of the graphs of the two given functions, we need to equate the functions.

`f(x)=g(x)\\\ln x=\ln x^2`

Two log functions with same base are equal only if their terms are equal to each other. Therefore,

`x=x^2\\\textrm{Subtracting x from both sides}\\x-x=x^2-x\\x^2-x=0\\x(x-1)=0\\\therefore x=0\ or\ x-1=0\\\therefore x=0\ or\ x=1`

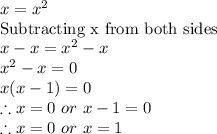
But a log function is not defined for
`x=0`. Therefore, the value of
`x` is only equal to 1.

Now, the
`y` value can be obtained using any one of the function.

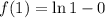`f(1)=\ln1-0` ( Since, log 1 = 0)

Therefore, the point of intersection of the functions
`f(x)\ and\ g(x)\ is\ (1,0)`.

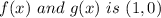The correct option is B. (1, 0).